Comp 2673, Spring 20003
Finite Automata, Part I

In the 1930's, long before the advent of modern computers, the question of computability began to be addressed. One of the main pioneers in this field was Alan Turing, who wanted to be able to formalize the idea of computability - precisely what types of questions can be answered with a computer? Turing personally believed that computers would ultimately be capable of independent thought - or at least would appear so to the outside observer. In order to address these questions, he invented a theoretical model for a machine (now known as a universal Turing machine). This machine, though simple, is capable of executing any algorithm or procedure that a modern computer can. When we talk about the theory of computability, we're merely interested in what can be accomplished, rather than the practicality or the speed of the implementation. Those questions are addressed in another branch of computer science, the study of computational complexity.

In this module, we'll study several models for computing, ending with what is known as the Turing machine. Since we're only interested in the theoretical capabilities of these machines, we don't worry at all about the implementations. They could be built mechanically out of gears, rotors and cranks (much like Charles Babbage did when he tried to build the first computing machine), or they could be constructed from transistors made photolithographically on wafers of silicon (as modern computers are). The important thing here is not how they operate physically, but rather how they model computation itself. In fact, implementations of these machines have been built mainly only for educational purposes. Modern computers can be made to simulate Turing machines - in other words, a computer can be programmmed to "act like" another type of computer. There are a few web pages available that contain simulations of Turing machines, and we'll use these to help us visualize that model of computation.

Finite State Automata The first model for computing we'll look at is Finite State Automata, or Finite State Machines. These machines are particularly suited to pattern recognition, but have other capabilities as well. A finite state machine consists of some fixed number of states or modes that the machine is in. The machine accepts a stream of input, and depending on the input and the current state of the machine, it switches to another state. This switching of states is called a transition. One of the states is labelled as the initial state, and one or some of the states are labelled as final states or accepting states. The machine cranks through the input, one at a time, potentially switching states at each step.

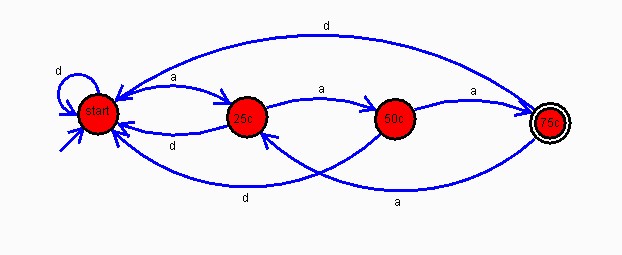
Example A simple practical example of a finite state machine is the inner workings of a soda machine. Imagine that sodas cost 75¢, and the machine accepts as input either insertion of a quarter or pushing the coin return button. When you walk up to the machine, the machine is in its initial state and is waiting for input. If you insert a quarter, the machine must "remember" that you did so, so it enters a new state, the "25¢" state. If you next insert a second quarter, the machine must again "remember" that you added another quarter, so it enters a new state, the "50¢" state. If you next press the coin-return button, it returns the coins and resets to the initial state. If, on the other hand, you added a 3rd quarter, the machine would accept your sequence of inputs as valid, and dispense a soda. At this point, it moves to the 25¢ state if you insert a quarter for the next soda, or it returns to the initial state if you press the coin return button. This primitive computation machine has a form of memory - it uses its current state as a way of remembering certain things about the past sequence of input.

A finite state machine can be represented with a drawing, called a state graph. The states are drawn as circles with a label, and arrows represent the transitions from state to state. The arrow points from the current state to the next state, and is labelled with the input that causes that transition. The initial state is indicated with an arrow pointing to it starting from empty space. The final state is drawn with a double circle. Below is a drawing of the soda machine fsa - in this drawing the input "a" means insertion of a quarter, and "d" means depressing the coin return button.

Try the following exercise on the soda machine fsa - what state are you in if you insert 4 quarters, depress the coin return, then insert 2 more quarters? Trace your way through the machine to check yourself. You can also simulate the action of this fsa using an automaton simulator web page. For example, link to Carl Burch's automata simulator. Download and run the program. Select "Deterministic Finite Automaton" under the "File" "New" menu. Note that you need to have Java installed on your machine to use this program.

Finite State Machines as pattern recognizers Finite State Machines are actually primitive computers. The type of computation they are best suited for is recognizing patterns. In fact, the soda machine fsa is just a pattern recognizer - it is searching for an input stream that ends with exactly 3 quarters in a row. It lands on the final state when it recognizes the pattern of exactly 3 quarters in a row at the end of the input stream. Let's design an fsa that can recognize a sequence of inputs that ends with "abba". It should land in the final state whenever the last 4 elements of the input stream are "abba". We say that the machine "accepts" all inputs ending in "abba".

Limitations on pattern recognition The exercises above show a few examples of input sets that you can design an fsa to recognize. Perhaps surprisingly, there are certain input sets that can't be recognized by any fsa. For example, suppose we want to design an fsa that accepts any string of inputs that have some number of 0's followed by the same number of 1's. It's a good exercise to try to design such an fsa and see what problems you run into. Now the fact that we try for an hour or two and fail, or even a week or two and fail, is no proof that such an fsa can't be designed. However, it has been proved that it's not possible to design such an fsa.

Languages There's an important relationship between finite state automata and languages. In order to examine this, let's first talk about the notion of a language. You're familiar with the idea of a natural language, such as English. If I asked the question "What exactly do we mean by the English language", one reasonable answer would be "It's the (huge) list of all the words and sentences from the English alphabet that are grammatically correct in English". For example, "onomatopoeia", "scrambled eggs", and "I want my Mommy." are all parts of this list, whereas "graxmurgo" and "Twins red flee cuddle mugwort." are not.

In computer science, there's an analogous idea of a language. A language is just a list of all finitely long sequences of letters in an alphabet (a finite set of symbols) that we'll define as "legal", or grammatically correct. This idea has some important applications.

Here are some examples of languages. The set of all computer programs written in C++ constitutes a language. The alphabet is the set of symbols used in the C++ language (such as a-z, A-Z, 0-9, |, %, etc.) A program that compiles is part of the language, while a program with a syntax error is not. Another example of a language is the set of all terminating decimal representations of numbers. Here, the alphabet is the set {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, .}, and examples of elements of this language include 3.14, 0.87345, and 456, while 2b|~2b and 12.34.56 are not part of the language. Another example of a language is the set of all strings of a's and b's that end with "abba". The string "baba" is not part of this language, but "bababba" is. A final example of a language is the set of all strings with some number of 0's followed by the same number of 1's. The string "1000110" is not part of this language, but "00001111" is.

Languages and Finite State Automata Notice that the language of all strings of a's and b's that end with "abba" is the same as the set of input strings that our second fsa recognized. In fact, any fsa accepts (or recognizes) a set of input strings, so any fsa recognizes a language. Therefore, we can think of an fsa as providing the definition of a language - any string that the fsa accepts is part of the language, and any string it doesn't accept is not part of the language.

On the other hand, recall the example of the language of all strings with some number of 0's followed by the same number of 1's. This is a language, but there is no fsa that recognizes it. So all fsa's have a corresponding language, but not all languages have a corresponding fsa. Which languages have a corresponding fsa? In other words, can you characterize which languages can be recognized by an fsa? This question was answered in 1956 by Stephen Kleene. Kleene's Theorem states that the languages defined by a regular expression are exactly those that can be recognized by some fsa.

Languages and regular expressions There's a big difference between natural languages and the types of languages we consider in computer science. While it is difficult to completely specify what constitutes valid speech in a natural language, in computer science we specify in a very rigorous way which sequences are part of the language. In English, most native speakers can be taken as experts in what constitutes an element of the language. However, there will be disagreements depending on geographical region, ethnic subculture, or economic class. You may choose to elect a usage panel who will determine in controversial cases what constitutes proper English, but there will always be cases that remain murky. In the field of computer science, however, we don't allow for ambiguous cases - our languages are specified rigorously and completely. For example, the syntax of C++ is absolutely clearly defined - there are no ambiguous cases. As you can imagine, this is extremely important, otherwise how could you write a compiler that would parse your program and accurately determine whether or not it had an error? To rigorously define a language, we give a list of rules that describe the legal elements. These rules are called grammar rules. Some languages are simple enough that the grammar rules can be indicated with a single expression (called a regular expression). This expression is essentially a pattern that every string in the language will match. Regular expressions are constructed with building blocks that allow for stringing together two or more expressions, choosing between two expressions, or repeating an expression multiple times. To show how this works, we'll look at a few examples of increasing complexity.

Examples of regular expressions that define a language In all of these examples, let's take the alphabet of the languages to be the set {a, b, c}. Remember that regular expressions are supposed to give a pattern for individual strings to match. We'll write regular expressions in bold letters, to distinguish them from ordinary strings. You should be able to design an fsa for each of these languages.

• In this first example, say that the only valid word in the language is "a". The regular expression we'll use to define this language is a. The only word that matches the pattern a is "a" itself.
• In the next example, say the language consists only of the words "a" and "b". The regular expression we'll use to define this language is a+b. Think of the + as "or", allowing you to choose between the expression on the left and the expression on the right. The only words that match the pattern a+b are "a" or "b".
• In this example, the only valid word is "ab". We are concatenating the individual words "a" and "b". The regular expression corresponding to this is just ab. Think of placing the two expressions together as a requirement that the string contains a match to the first expression followed by a match to the second expression.
• In the next example, our language is the set of words containing one more more a's (and no other letters). In other words, the valid words are "a", "aa", "aaa", etc. The regular expression to describe this is a⁺. Think of the superscript ⁺ as indicating that the string contains one or more matches to the expression in a row.
• Now let's say our language is any word consisting of some number of a's (including none). In other words, the valid words in the language are "" (the empty word), "a", "aa", "aaa", etc. The regular expression to describe this is a^*. Think of the superscript ^* as indicating that the string contains zero or more matches to the expression in a row.
• If we have any two regular expressions, we can connect them with a +. This means that we'll accept any string that matches the first expression or that matches the second expression. For example, the regular expression c⁺+b⁺ describes the language of nonempty words that are either all c's or all b's (that is, "c", "cc", "ccc",..., "b", "bb", ...).
• If we have any two regular expressions, we can connect them by concatenating. For example, if we concatenate the regular expressions b+c and a^* to get the regular expression (b+c)a^*, this defines the language of all words that have a single b or c, followed by zero or more a's. (that is, "b", "ba", "baa",..."c", "ca", "caa",...).
• If we have a regular expression, we can give it a superscript ⁺. This means that we'll accept a string containing the concatenation of one or more strings that match the expression under the ⁺. For example, the regular expression (a+c)⁺ defines the languages of all nonempty strings containing only a's and c's.
• If we have a regular expression, we can give it a superscript ^*. As before, this acts much like a ⁺ superscript, except that we'll accept a string containing the concatenation of zero or more strings that match the expression under the ^*. For example, the regular expression b(a+c)^* defines the languages of all strings that start with the letter b, and are followed by any number (including none) of a's and c's. So "b", "ba", "bc", "baaa", "bca", etc. are all in the language, whereas "acc", and "bab" are not.
• Note that if w is a regular expression, then w⁺ is equivalent to ww^*

• The language of all words from the input alphabet {0, 1} that begin with a 0 and end with a 1 is given by the regular expression 0(0+1)^*1.
• The language defined by the soda machine fsa (all words that end with exactly 3 a's in a row) is given by (d+ad + aad + aaa)^*aaa
• The language from the input alphabet {1, 2} in which every word has a number of 1's that's divisible by 3 is given by (2^*12^*12^*12^*)^*.

• Make a finite state machine that accepts any string from the alphabet {0, 1} that starts with 0 and ends with 1, and outputs the value just input. Show the output string for the input string 01010011, and write the regular expression that goes with the machine it.
• Create a finite state machine that inputs strings from the alphabet {x, y} and outputs EE, OE, EO, or OO, depending on the parity of the number of x's and y's, and accepts strings that contain an even number of x's and y's. For example, the string xxyyx has an odd number of x's and an even number of y's, so the output would be OE, and the string would not be accepted.