Comp 2673, Spring 20003
Turing Machines

We've seen how finite state machines can be used to perform simple computation such as pattern matching. We also saw how this computation is limited. For example, a finite state machine cannot be used to recognize the language {anbn| n>0 }. Similarly, it's impossibnle to design a finite state machine that recognizes the language of nested parentheses that are matched.

The states and transitions of a finite state machine can be viewed as a primitive CPU. A finite state machine also has input and possibly output. However, a finite state machine does not have memory, and this is what limits its capabilities. There are different types of memory that we could add, resulting in different types of machine. In this section, we will add a type of random-access memory to the finite state machine.

A Turing machine is a finite state machine with an additional component of memory. The memory of a Turing machine is a tape divided into cells that stores a sequence of symbols. The symbols come from the input/output alphabet, which also contains a blank symbol. Only finitely many of the cells on the tape are non-blank at any given time. The tape continues infinitely in both directions. Initially, the input to the machine is stored on the tape. At each step, the machine reads the input from the current position on the tape, writes an output symbol on the current position of the tape (or leaves it the same as it was), moves the tape either right or left by one cell, and then transitions to a new state, The output symbol and the direction to move are included in the definition of a transition. If for some state, the list of transitions doesn't include an entry for a particular input, then when the machine is in that state and that input is encountered, the machine halts. Note that when it halts, it may or may not be in a final (accepting) state.

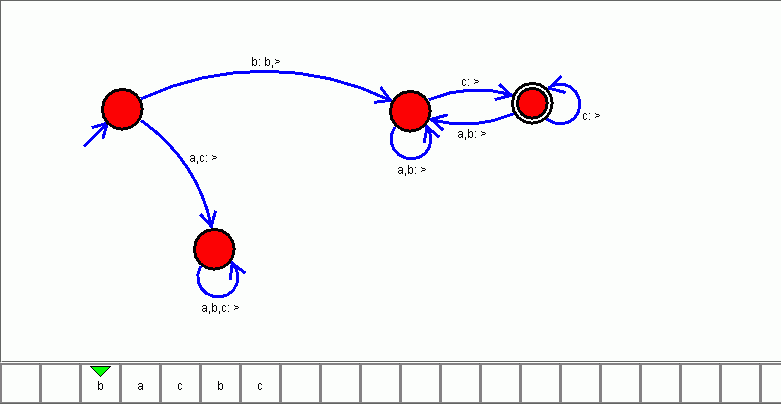
A Turing machine can be used to everything that a finite state machine does. At each step, the Turing machine reads the input from the tape, writes the output back to the tape, and steps the tape to the right. For example, here's a turing machine that accepts the language of words that start with b and end with c.

A turing machine that increments

A turing machine that recognizes the language {anbn}

A turing machine that copies

Here's a turing machine that makes a copy of a binary number. The program is written in 3 forms, first, a graphical picture, second a sequential program and third a list of transitions and initial/final states. There is no difference between any of these programs - they are just different ways of displaying the same turing machine. 

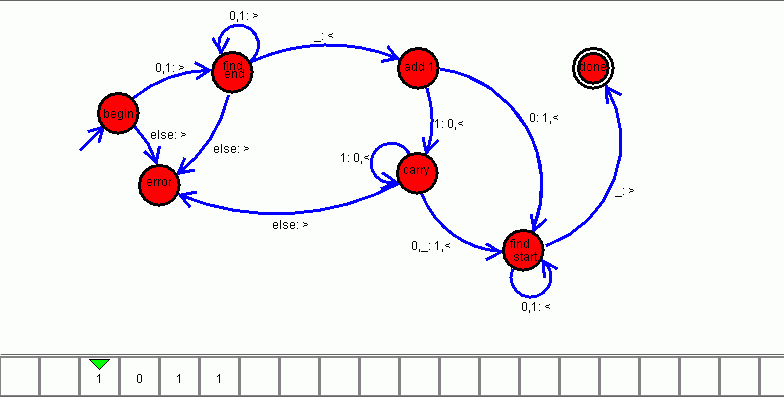
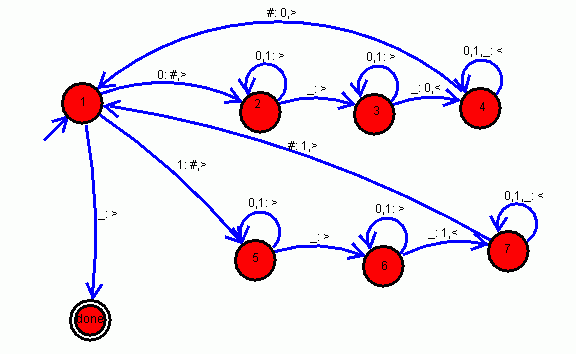
Sequential program:
1: if input == '0', output '#', move right, goto line 2
   if input == '1', output '#', move right, goto line 5
   if input == ' ', don't change symbol, move right, goto line 8
2: if input == '0' or '1', don't change symbol, move right, goto line 2
   if input == ' ', don't change symbol, move right, goto line 3
3: if input == '0' or '1', don't change symbol, move right, goto line 3
   if input == ' ', write a '0', move left, goto line 4
4: if input == '0', '1', or ' ', don't change the symbol, move left, goto line 4
   if input == '#', write a '0', move right, goto line 1
5: if input == '0' or '1', don't change symbol, move right, goto line 5
   if input == ' ', don't change symbol, move right, goto line 6
6: if input == '0' or '1', don't change symbol, move right, goto line 6
   if input == ' ', write a '1', move left, goto line 7
7: if input == '0', '1', or ' ', don't change the symbol, move left, goto line 7
   if input == '#', write a '1', move right, goto line 1

List of transitions (start state, input, end state, output, movement)
(1, '0', 2, '#', >)
(1, '1', 5, '#', >)
(1, ' ', 8, ' ', >)
(2, '0', 2, '0', >)
(2, '1', 2, '1', >)
(2, ' ', 3, ' ', >)
(3, '0', 3, '0', >)
(3, '1', 3, '1', >)
(3, ' ', 4, '0', <)
(4, '0', 4, '0', <)
(4, '1', 4, '1', <)
(4, ' ', 4, ' ', <)
(4, '#', 1, '0', >)
(5, '0', 5, '0', >)
(5, '1', 5, '1', >)
(5, ' ', 6, ' ', >)
(6, '0', 6, '0', >)
(6, '1', 6, '1', >)
(6, ' ', 6, '1', <)
(7, '0', 7, '0', <)
(7, '1', 7, '1', <)
(7, ' ', 7, ' ', <)
(7, '#', 1, '1', >)
Start state: 1
Accepting state(s): 8
The above example shows that even copying a number from one spot to another can be a little complicated. However, a turing machine can be created that accomplishes any tasks you've seen a modern computer perform. For example, you could create a turing machine that took as input the list of transitions given above, and used it to simulate a turing machine with those transitions. Such a machine is known as a universal turing machine. This is one level of abstraction beyond what we've done so far. Instead of making a turing machine, you just use the universal turing machine and feed it the list of transitions for the machine you want to create. It then simulates the turing machine with the transition diagram you gave it as input. Creating the list of transitions is known as "programming". The programmable universal turing machine is thus a truly programmable computer and is capable of performing any task a modern computer does. The only difference is speed.