Graph Theory, Part II

Paths, Circuits, and Cycles

A path is a list of vertices in a graph, directed graph, or weighted graph. For each adjacent pair on the list, that corresponding edge must be in the graph. The length of a path in a graph or directed graph is the number of edges in the path. For example, consider this graph:

The sequence 4 → 5 → 6 is a path of length 2, while the sequence 1 → 2 → 3 is not a path. There is no path from 1 to 6. In the following directed graph

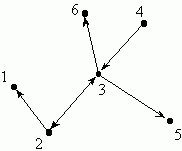
The sequence 4 → 3 → 2 → 1 is a path of length 3, while 5 → 3 → 2 → 1 is not a path.

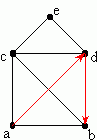
In a weighted graph, the length of a path is the sum of the weight of each of its edges. In the following weighted graph,

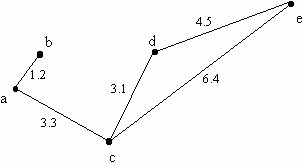
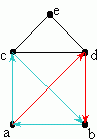
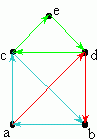
the path b → a → c → d → e has total weight 1.2 + 3.3 + 3.1 + 4.5 = 12.1. It is not the shortest path from b to e, since the path b →a → c → e has total weight 1.2+3.3+6.4 = 10.9. (Note that some textbooks use the word trail for what we have just described, and reserve the word path for trails in which no edge appears more than once.) A circuit is a path that starts and ends at the same vertex. A cycle is a circuit that does not repeat any edges. For example, in the weighted graph above, c → d → e → c is a cycle.

Connectedness

A graph is connected if for each pair of vertices a and b, there is a path in the graph starting at a and ending at b. The graph at the top of this page is not connected. The weighted graph shown above is connected.

Trees

A tree is a connected graph containing no cycles. Here is an example of a tree:

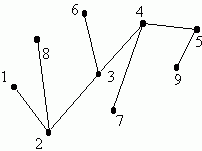
(Note: some texts require that you designate one node of a tree as the "root" node.) There are many conditions that turn out to be equivalent to the "connected and acyclic" requirement. The following are each equivalent conditions for a graph G. This means that any of them could have been used as the definition of tree. Check that each of them holds in the example tree drawn above.

• G is a tree (G is connected and acyclic)
• G is connected, but the removal of any edge from G disconnects G into two subgraphs that are trees.
• G contains no cycles, and the number of vertices is one more than the number of edges.
• G is connected and the number of vertices is one more than the number of edges.

Multigraphs

In a multigraph, we allow potentially more than one edge between two vertices. This would be useful if the nodes represents cities, and the edges represent daily plane flights between them. If there were 4 flights from Denver to Chicago each day, we could represent this with 4 edges. If the nodes represent locations on a map and the edges represent roads between them, then if there are two or more different roads connecting two points, we could represent that with multiple edges between them. If the nodes represent atoms and the edges represent chemical bonds, then we can represent a double or triple bonds with two or 3 edges. Here's an example of a multi-graph.

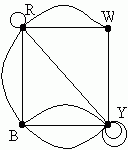
(Note: graph theory can be used to help solve the game "Instant insanity", in which you try to arrange 4 multi-colored cubes in a column of 4 so that each color appears on each side of the column. The above multi-graph is part of the solution.)

Degrees of vertices

In a graph or a multi-graph, the degree of a vertex v (written deg(v)) is the number of edge ends at that vertex. For example, in the multi-graph above, deg(W) = 3, deg(B)=5, deg(R) = 7, and deg(Y) = 9.

The Königsberg bridge problem

Leonard Euler began the study of graph theory. He was inspired to begin the study by the Königsberg bridge problem. Legend has it that in the early 1700's it was a popular weekend pasttime in Königsberg (now Kaliningrad) to stroll around the city trying to find a path that crossed exactly once each one of the 7 bridges over the Pregel River, and then returned to the starting point. Here's a web page shows a map of Königsberg from that era: Königsberg's bridges. Euler invented graph theory in order to solve this problem, and he succeeded in solving it in 1736. He modeled the bridges with edges in a multigraph, the nodes representing the regions on the city. Here is a multigraph that represents the layout of the cities bridges:

Euler paths and Euler circuits

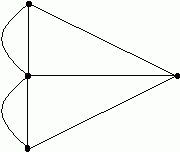
An Euler path is a path in a graph that traverses each edge exactly once. An Euler circuit traverses each edge exactly once and ends at the vertex at which that it started. The Königsberg bridge problem asks you to find an Euler circuit. Can you find a solution? It's similar to a kid's puzzle that asks you to draw this picture of a house without lifting your pencil:

This time the problem is to find an Euler path. When does such a path or circuit exist, and when doesn't it? Euler answered this question with the following theorem.

Theorem on Euler paths An Euler path exists in a connected graph if and only if there are either no vertices of odd degree, or exactly two vertices of odd degree. In the case of no vertices of odd degree, then the path may start at any node, and will end where it started (giving an Euler circuit). In the case of two nodes of odd degree, the path must start at one of them and will end at the other.

Thus, there is a solution to the house picture, and every solution in the house picture must start and end at the bottom two nodes. In the other hand, the Königsberg bridge problem has no solution.

There is an algorithm for constructing an Euler circuit (or Euler path), if it exists. The procedure is recursive.

• Step 1: Start by finding any circuit in the graph (or any path from one of the odd-degree vertices to the other) that doesn't re-use edges. If the circuit (or path) you chose uses all of the edges, you're done. If the circuit (or path) you have doesn't use all the edges, then remove from the graph each of the edges you used in your circuit (or path). You'll be left with edges that form a subgraph - it will have only even-degree vertices, so each of its components has an Euler circuit of its own.
• Step 2: Find an Euler circuit in each of the components of the subgraph (this is the recursive step).
• Step 3: Splice your subgraph Euler circuit(s) from step 2 into your original circuit (or path) from step 1. To do this, just follow your step 1 circuit (or path) until you first hit a node that lies in your subgraph Euler circuit(s). Take a detour around the entire subgraph Euler circuit, then complete the original circuit.

• Step 1 is to find a path, any path, from one of the odd-degree vertices to the other that doesn't reuse edges. I choose a → d → b. Since I didn't happen to end up with an Euler path, I remove those edges from the graph to get a subgraph. I've drawn the removed path in red, the subgraph is still black:

  

• Step 2 is to find an Euler circuit in the subgraph. There are, of course, three steps to this process.
  • Step 1 is to find any circuit in the graph that doesn't re-use edges. I choose b → a → c → b. Since this is not itself an Euler circuit, I remove these edges from the graph to get this subgraph. I've drawn the removed circuit in light blue, the remaining subgraph is stil black:

    

  • Step 2 is to find an Euler circuit in the subgraph. I recursively begin the procedure again:
    • Step 1 is to find any circuit in the graph that doesn't re-use edges. I choose d → c → e →d. This is an Euler circuit! I can skip steps 2 and 3.

      

  • Step 3 is to splice together my circuit from the corresponding step 1: b → a → c → b (light blue) with the Euler circuit d → c → e → d (green). I travel along the circuit from step 1 until I hit a vertex contained in the Euler circuit. I'll mark that point with a * to show where I will splice in the Euler circuit: b → a → c* → b. At the *, I insert the Euler circuit from my lastest step 2, starting and ending at vertex c. The blue and green paths together have given me b → a → c → e → d → c → b.
• Step 3 is to splice together the path a → d → b (red) from step 1 and the Euler circuit b → a → c → e → d → c → b from step 2. I'm now supposed to travel along the step 1 path until I hit a vertex on the circuit. However, the first node in the path already lies on the Euler circuit. So I travel along the entire Euler circuit first from a back to a, then complete the (red) path from step 1. My final path is a → c → e → d → c → b → a → d → b.