Dijkstra's Shortest Path Algorithm
It's an important problem of graph theory to find the shortest path between two vertices. In a weighted graph, we're looking for the path for which the sum of the weights of the edges along the path is as small as possible. Because weights often represent distance, we call this the shortest path. In a graph or directed graph, we're looking for the path with the fewest edges. This problem is important in communications, where information must be sent between nodes in the fastest possible way, or in transportation, where we need to find the most efficient route to transport goods between different locations. This problem is an example of an optimization problem - we want to find the minimum path length. Optimization problems in the discrete settings of computer science tend to be much more difficult than in the continuous settings you've seen in calculus. For many simple optimization problems (such as the travelling salesman problem) there are no good solutions. However, for the shortest-path problem, there turns out to be a good solution - an algorithm called Dijkstra's algorithm.
Say that v0, v1, ..., vn are the vertices in a connected graph. Our goal is to find the shortest path from v0 to vi. We'll call the length of this path the distance from v0 to vi and write it d(v0, vi). As part of this process, we'll end up finding the shortest path from v0 to many of the other nodes as well (and thus the distance from v0 to the other nodes).
The algorithm is based on this observation: If the path
v0 → w1 → w2 → ... →
wn → vi is the shortest path from
0 to vi, then the path
v0 → w1 → w2 → ...
→ wn is the shortest path from v0 to wn.
We will use this idea to build shortest paths starting
at v0 and ending at various vertices. We'll find them in order of
each vertex's distance to v0.
First, the distance from v0 to itself is 0. So v0 is
handled - we'll put it into the list of vertices for which we've
found the shortest path. Now find the closest vertex reachable from
v0 with one edge. This means checking for each vertex vi
the following value:
weight(v0, vi)
and choosing the smallest one.
Call that vertex w1. The distance from
v0 to w1 (written d(v0, w1))
is just the weight(v0, w1).
We're now done with w1. We move on now to the next-closest
vertex. It must pass through w1, or through no intervening nodes
at all. So for each vertex vi, we'll just check the values
weight(v0, vi)
d(v0, w1) + weight(w1, vi)
and pick the smallest. Call this vertex w2,
and we have calculated d(vi, w2). We're now done
with
the vertex w2. The next step is to find the next closest vertex.
The shortest path to the next-closest vertex has its penultimate
(second-to-last) vertex
in the list {v0, w1, w2}, the list of
done vertices. So we just just check, for each vertex vi,
the following valuesIn order to implement this algorithm, we'll have to store some information as we go. There are many ways to organize the information you collect as you proceed with your algorithm that will make it more efficient. Here is one way. At each step, for each vertex, store both your current best distance to that node and the previous node you should pass through to get to it. At each step, also store your list of vertices that you're done with (those for which you've already found the shortest path). For each vertex, check to see if passing through the latest "done" vertex shortens the path. In other words, if wlatest is the latest "done" vertex, then for each vertex vi, check d(v0, wlatest) + weight(wlatest, vii, then update the distance and previous node for vi. Finally, go through the list of vertices that have not been handled yet, and choose the closest one. Add it to the list of "done" vertices.
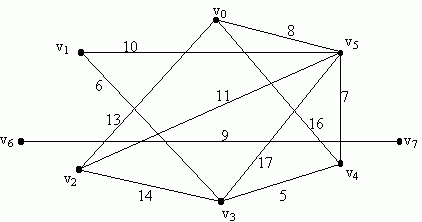
Here's an example. We'll find the shortest path from v0 to all other vertices in this graph.

| Step # | v0 | v1 | v2 | v3 | v4 | v5 | v6 | v7 | Next closest vertex: |
|---|---|---|---|---|---|---|---|---|---|
| 0 | (0, v0) | (∞, -) | (∞, -) | (∞, -) | (∞, -) | (∞, -) | (∞, -) | (∞, -) | v0 |
| 1 | (∞, -) | (13, v0) | (∞, -) | (16, v0) | (8, v0) | (∞, -) | (∞, -) | v5 | |
| 2 | (18, v5) | (13, v0) | (25, v5) | (15, v5) | (∞, -) | (∞, -) | v2 | ||
| 3 | (18, v5) | (25, v5) | (15, v5) | (∞, -) | (∞, -) | v4 | |||
| 4 | (18, v5) | (20, v4) | (∞, -) | (∞, -) | v1 | ||||
| 5 | (20, v4) | (∞, -) | (∞, -) | v3 | |||||
| 6 | (∞, -) | (∞, -) |