Comp 2673
Homework 3 Solutions
Topic: Graph theory
  1. Here's the graph described by the edge list:

  2. V = {a, b, c, d, e, f}
    E = {(a,d), (a,e), (b,d), (b,e), (b,f), (c,e), (c,f), (d,e), (e,f)} 
  3.       a    b    c    d    e    f
    |-                          -|
  a | 0    0    0    1    1    0 |
  b | 0    0    0    1    1    1 |
  c | 0    0    0    0    1    1 |
  d | 1    1    0    0    1    0 |
  e | 1    1    1    1    0    1 |
  f | 0    1    1    0    1    0 |
    |_                          _|
  4. d → e → c
  5. The graph has 6 vertices, and so any tree must have 5 edges. We start with 9 edges, so we have to remove 4 edges.
  6. Here's the graphs for problem 6:

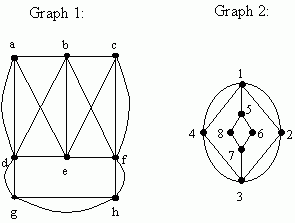
    In graph 2, there are 4 vertices of odd degree (1, 5, 7 and 3), so there is no Euler circuit or Euler path. In graph 1, there are exactly two vertices of odd degree (b and e), so there is an Euler path. It starts at b and ends at e, or vice versa. Using the algorithm for finding Euler paths, we starting by choosing any path from b to e. For example, we could start with
    b → c → f → h → g → d → a → e
    Here's what remains:

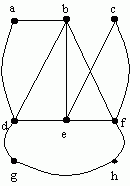
    The next step is to find an Euler circuit in what remains. We'll start with any circuit, for example
    a → b → f → h → g → d → a
    Here's what now remains:

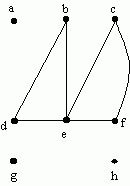
    and an Euler circuit through this is
    b → e →c → f → e → d → b
    Splicing the last circuit into the second-to last gives
    a → b → e →c → f → e → d → b → f → h → g → d → a
    Finally, shift this circuit to start at b, and splice it into the start of the original path, giving
    b → e →c → f → e → d → b → f → h → g → d → a → b → c → f → h → g → d → a → e

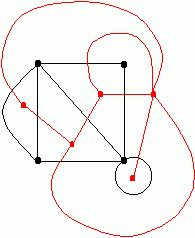
  7. For the graph shown, there are 4 vertices, 5 regions, and 7 edges. v-e+r = 4-7+5 = 2, as expected. Here's a picture of the dual, in red.


    In the dual, there are 5 vertices, 4 regions, and 7 edges. Now v-e+r=5-7+4 = 2.

  8. In the first pair, the two graphs are isomorphic, which we see by corresponding the vertices a with 3, b with 4, e with 2, c with 1, and d with 5. There are other possibilities for how to do the correspondence.
    In the second pair, the two graphs are not isomorphic, because the first graph is not connected and the second graph is. Also, in the second graph there is a vertex of order 4, and in the first graph there is not.
    In the third pair, the two graphs are not isomorphic, because in the first graph the longest cycle is of length 4, while in the second graph the longest cycle is of length 5.


  9. Step # a b c d e f g Next closest vertex:
    0 (0, a) (∞, -) (∞, -) (∞, -) (∞, -) (∞, -) (∞, -) a
    1 (14, a) (∞, -) (∞, -) (17, a) (∞, -) (10, a) g
    2 (13, g) (∞, -) (14, g) (16, g) (∞, -) b
    3 (22, b) (14, g) (16, g) (24, b) d
    4 (22, b) (15, d) (21, d) e
    5 (22, b) (21, d) f
    6 (22, b) c