Comp 2673, Spring 20003
Homework 6
Due June 2, 2003

1. Design a finite state automaton that accepts any string of inputs ending in "abab". The alphabet is {a, b}.
2. Below is a finite state automaton. Determine the set of inputs that puts it in the final state (i.e., the set of inputs that the machine "accepts".) Describe this set in words, then give a regular expression that defines it.
   
3. Design a finite state automaton that accepts any input in which the total number of "1"s is divisible by 3. The alphabet is {0, 1}.
4. Describe the language accepted by the fsa shown below, then write a regular expression defining this language.
   
5. Design a finite state automaton with output that gives a 2-unit delay. The input alphabet is {0, 1}. In other words, it outputs the input from two steps previous. It's not necessary to give it a final (or accepting) state. You should need 4 states. How many states are required for a 3-unit delay? An n-unit delay?
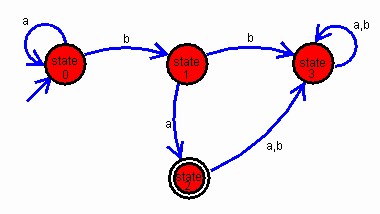
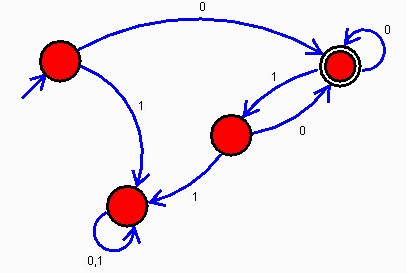
6. Create a Turing machine that does the following. Assume the input is a string of 1's and 0's representing a binary number n. The number is bounded on the left by a blank and terminated with a blank. The purpose of the machine is to calculate 2n-1. For example, suppose that the string stored on the tape is

    ' 1010 '
      ^         (This mark shows the start position)
   

   This represents the number 6. After the turing machine halts in an accepting state, the tape should look like

    ' 10011 '
      ^
   

   representing the number 11 (eleven). After completing the calculation, the turing machine should reposition the head to point to the beginning of the number.