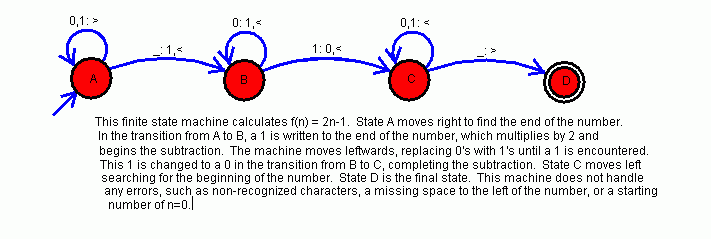
Comp 2673, Spring 2003, Homework 6 solutions

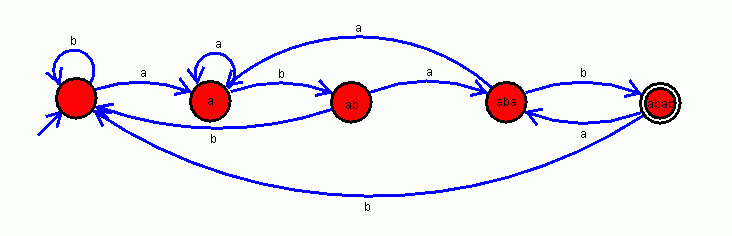
Here's a finite state machine that accepts any string of inputs ending in "abab", where the alphabet is {a, b}
The machine given in the assignment accepts any string from the alphabet {a,b} that contains exactly one b, and ends with an a. Another way to word it is that the string starts with an arbitrary number of a's (possibly none), followed by ba. The regular expression that defines this is a^*ba.
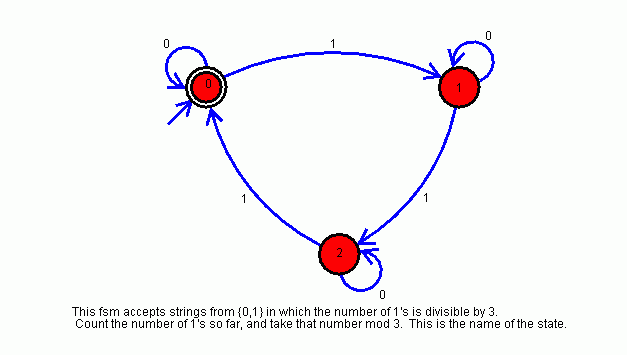
For the fsm that accepts any string in which the number of 1's is divisible by 3, most of you neglected strings with NO 1's. For example, the machine should accept the string "000". To solve this problem, make the initial state the accepting state.
The next machine given in the assignment accepts any string from the alphabet {0,1} that starts and ends with 0, and in-between never has two 1's in a row. Another way to word it is that the string starts with 0, and is followed by any arbitrary number of either 0's or 10 pairs. The regular expression that defines this is 0(10+0)^*. Note that there are other possibilities for regular expressions that define the same language.
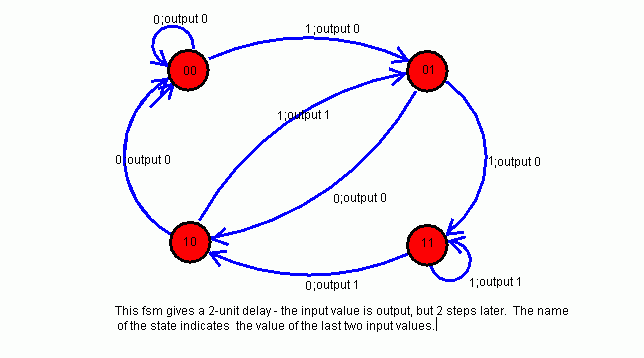
Assuming that we start by outputting two 0's, and assuming that we don't handle the end of the string, a 2-unit delay takes 4 states, a 3-unit delay takes 8 states, and an n-unit delay takes 2ⁿ states.
Solution: