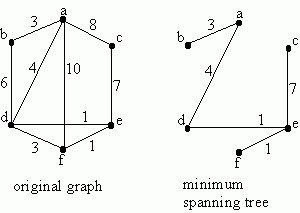
There are a couple of efficient algorithms for finding a minimal spanning tree. One of these is known as Kruskal's algorithm. This lab will give you practice with Kruskal's algorithm.

Kruskal's algorithm is pretty straight-forward. You choose edges one at a time to put into the tree. Start by choosing the shortest edge (the edge with the smallest weight) and put that into your graph. If there are multiple edges with the same weight, then choose any one of them. Now consider the edges that remain, and choose the shortest which, when you add it to your graph, does not create a cycle. Continue in this manner, adding the shortest edge which does not create a cycle, until your tree is connected. Recall that if a graph has n vertices, then a tree has n-1 edges. This means that you'll need to select a total of exactly n-1 edges before you're done.

1. Consider the following weighted graph.

   

   Run the graph through Kruskal's algorithm (by hand). List the edges you added in order. What is the total weight of the minimal spanning tree?

2. Go to the website Kruskal's algorithm. Go to the bottom of the page, where you'll find a Java applet that calculates minimum spanning trees using Kruskal's algorithm. Input the above graph, and see what mimimal spanning tree results.
3. Now run the graph below through Kruskal's algorithm (by hand). Draw a minimum spanning tree that results. What is the total weight? Input it into the program on the website, and see what minimum spanning tree it gives. Is it the same tree? What is the total weight of the tree the website gives?

   

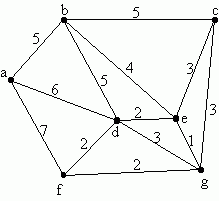
4. Extra credit: How many possible mimimum spanning trees are there for the above graph?
5. Extra credit: For the previous graph, list the weights of the edges added in Kruskal's algorithm in order. Do the same for one of the other possible mimimum spanning trees. Can you find a mimimum spanning tree with a different sorted edge list?