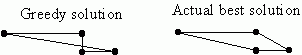
Often we assume that the nodes (cities) lie in a plane and the weight of each edge is just the (Euclidean) distance between them. We use the complete graph, meaning there's an edge between each pair of nodes. In other words, you may travel directly between any two cities.
The two graph-theory algorithms you've seen so far (Kruskal's algorithm for minimum spanning tree and Dijkstra's algorithm for shortest path) are both greedy algorithms. The crucial step in each algorithm is to choose the next-best (this is why they're called "greedy"). In the case of Kruskal's algorithm, we choose the next lightest edge that doesn't create a cycle. In Dijkstra's algorithm, we choose the next-shortest path that uses only vertices we're done with. Despite the simplistic approach of these algorithms they succeed in finding the best solution. For the travelling salesman problem, you might try a greedy approach - for example, you might try following a path that always goes to the next-closest unused node. However, this greedy approach does not work - it simply does not find the best path. Here's an example that shows the path that a greedy approach would choose, versus the true shortest path:
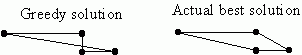
The only known solution to the travelling salesman problem is the brute-force approach. This means trying every possible route. Let's figure out how many routes need to be tried if there are n cites. Assume that the start city is fixed. There are n-1 choices for the 2nd city, n-2 choices for the 3rd city, etc. Thus, there are (n-1)· (n-2)·...·3·2·1 = (n-1)! possible routes. Assuming that we calculate the distances between each city in advance, then each route requires n additions. This means we need about n! additions to solve the problem. In other words, this algorithm is o(n!) Assuming that we can do 500 million floating point operations per second, the following table shows how long it will take to solve the travelling salesman problem for various numbers of cities.
| n | # of routes | # of additions | time to compute |
|---|---|---|---|
| 3 | 2 | 6 | 12 nanoseconds |
| 4 | 6 | 24 | 48 nanoseconds |
| 5 | 24 | 120 | 240 nanoseconds |
| 6 | 120 | 720 | 1.4 microseconds |
| 7 | 720 | 5040 | 10 microseconds |
| 8 | 5040 | 40320 | 81 microseconds |
| 9 | 40320 | 362880 | 726 microseconds |
| 10 | 362880 | 3628800 | 7 milliseconds |
| 11 | 3.6 million | 40 million | 80 milliseconds |
| 12 | 40 million | 480 million | .96 seconds |
| 13 | 480 million | 6.2 billion | 12.5 seconds |
| 14 | 6.2 billion | 87 billion | 3 minutes |
| 15 | 87 billion | 1.3 trillion | 44 minutes |
| 20 | 1.22 × 1017 | 2.4 × 1018 | 154 years |
| 25 | 6.2 × 1023 | 1.6 × 1025 | 984000 millenia |
Actually, there are ways to improve the discouraging numbers shown above.
The brute force solution can be made more efficient by recognizing poor
solutions
before checking them, and thus reducing the amount of computation needed.
The best brute-force solutions so far are of exponential order in the
number of nodes. This is a significant improvement over a
factorial order, which makes the solution accessible for larger numbers
of nodes. However, the problem is still intractable past about 150 nodes.
Here is a web site that has an excellent exhaustive search solution to
TSP.
TSP exact solution - very efficient
When you're doing an exhaustive search, you must try every permutation of
nodes.
However, sometimes after listing just the first few nodes in the path, you
can already realize that it can't be better than your best so far. One
way to do this is to add the lengths of those first few nodes, then get
a lower-bound for the path through remaining nodes. If the sum of the
start of the path and the lower-bound for the rest of the nodes is larger
than your best so far, then you can omit testing ALL of the paths that
begin with those first few nodes.
This is sometimes called branch-and-bound, and it can
drastically reduce the number
of paths you have to check. To find a lower bound for a path through the
remaining nodes, you can find a mimimum spanning tree. Since any path
through the remaining nodes will connect them, the sum of those lengths
can't exceed the mimimum spanning tree (taking into account the two edges
that connect the unused nodes to the start of the path). You know how
to find the MST already - use Kruskal's algorithm. This technique can
be further improved by finding a really excellent route before you even
begin. The length of this first route is the one try to beat - the better
it is, the more paths you'll avoid checking. Therefore, in order to
find the absolute optimum route, it is helpful to start by finding
a very very good one.
Because the computational complexity of the exhaustive search is exponential,
for many real-world applications people are willing to trade
finding the very best solution in exchange for a pretty good solution that
can be found quickly. Many algorithms have been developed to do this.
These are sometimes known as heuristic algorithms. Examples include
the techniques of simulated annealing, genetic algorithms, memetic
algorithms, neural networks, dynamic programming, clustering techniques,
and others. These techniques can also be used in combination, and
each have a wide range of applications other than TSP.
Later this quarter, we'll talk about the genetic alogorithm solution
to the travelling salesman problem.