West Coast Operator Algebra Seminar 2014

Please find all the talks, with their titles, abstracts and slides. The slides are provided courtesy of the speakers, and can be accessed on clicking on the thumbnail of the first slide.

If you click on the following thumbnail, you will access a PDF copy of the conference brochure.

Gene Abrams, University of Colorado at Colorado Springs

Talk Title:	An introduction to Leavitt path algebras, with connections to C$^*$-algebras and noncommutative geometry
Talk Abstract:	Since 2005, a class of algebras, the {\it Leavitt path algebras} $L_K(E)$ (for $K$ any field and $E$ any directed graph), has been the focus of significant research attention. The $\mathbb{C}$-algebra $L_{\mathbb{C}}(E)$ can be viewed as forming the algebraic underpinnings of the graph C$^*$-algebra $C^*(E)$. In this talk I'll define these Leavitt path algebras, and give some of their general properties. I'll describe two instances where results about Leavitt path algebras have led to a deeper understanding of the structure of graph C$^*$-algebras. Then I'll describe some of the current lines of investigation in the area. One such line is the search to understand the still-mysterious similarities between structural properties of $L_{\mathbb{C}}(E)$ and those of $C^*(E)$. Another such line is the search for an analog to the Kirchberg Phillips Theorem in this context. Finally, I'll describe how the algebras $L_K(E)$ arise naturally in the context of various questions about noncommutative algebraic geometry.
Talk Schedule:	Saturday 11/1, 3:00pm

Heath Emerson, University of Victoria

Talk Title:	Poincare duality for C*-algebras and applications
Talk Abstract:	Poincare duality in homology is exhibited by smooth, compact, oriented manifolds. One application of duality is to the Lefschetz fixed-point formula and its variants. An important observation in the context of Index Theory was that, suitably formulated, Poincare duality is present in K-theory as well, if the orientation assumption on the manifold is strengthened suitably. As noncommutative geometry has developed, a number of examples of noncommutative C*-algebras exhibiting K-theoretic duality have emerged as well. What about the Lefschetz fixed-point formula? We state a general analogue of the Lefschetz fixed-point formula for C*-algebras satisfying duality, which works equivariantly as well, and which when specialized to the commutative case, generalizes the classical formula -- making it equivariant with respect to an action of a connected compact Lie group, and applying to smooth correspondences, rather than just maps.
Talk Schedule:	Saturday 11/1, 10:00am

Shane Farnsworth, Perimeter Institute

Talk Title:	Rethinking Connes' approach to the standard model of particle physics via non-commutative geometry
Talk Abstract:	Connes has argued that non-commutative geometry (NCG) more aptly describes the standard model Lagrangian. Although his papers have generated enormous interest, many physicists are skeptical because: (i) NCG relies on a long list of axioms whose meaning is obscure to them; and (ii) the NCG construction of the standard model Lagrangian relies on a fishy step where 7 problematic terms must be set to zero, essentially by hand, to get the desired result. In this talk I discuss a simple reformulation of Connes' ideas with two key advantages: (i) it fixes both above mentioned problems: the axioms are dramatically simplified and unified, while the 7 problematic terms are precisely eliminated; and (ii) it immediately generalizes from non-commutative to non-associative geometry. (arXiv:1401.5083, arXiv:1408.5367)
Talk Schedule:	Sunday 11/2, 09:00am

Eusebio Gardella, University of Oregon

Talk Title:	Rigidity results for L^p-operator algebras.
Talk Abstract:	Algebras of operators on L^p-spaces (for $1 \leq p < \infty$) have recently received a great deal of attention. Their systematic study initiated by Phillips was soon followed by the work of other authors (Pooya-Hejazian, G.-Thiel, G.-Lupini, Phillips-Viola, and more). Despite the absence of adjoints, much of the theory so far developed resembles and is inspired by the theory of C*-algebras. Nevertheless, it is becoming apparent that L^p-operator algebras, for $p\neq 2$, are far more rigid objects than C*-algebras, even when they 'look like' C*-algebras. In this talk, we will discuss some rigidity results concerning L^p-operator algebras, focusing on the L^p-analog $F^p_\lambda(G)$ of the reduced group algebra of a locally compact group $G$. (These algebras were introduced a long time ago by Herz, who called them algebras of $p$-pseudofunctions on $G$.) The main result of the talk is that for $p,q\in [1,\infty ) \setminus \{2\}$, and for second countable locally compact groups $G$ and $H$, there is a contractive isomorphism $F^p_\lambda(G)\cong F^q_\lambda(H)$ if and only if $p$ and $q$ are either equal or conjugate, and $G$ is isomorphic to $H$. For $p=q=1$, this result was proved by Wendel in the 60's. This is based on joint work with Hannes Thiel (University of Muenster).
Talk Schedule:	Sunday 11/2, 11:00am

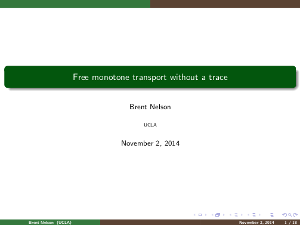
Brent Nelson, UCLA

Talk Title:	Free monotone transport without a trace
Talk Abstract:	Classically, transport between probability spaces $(X,\mu)$ and $(Z,\nu)$ is a measurable map $T:X\to Z$ such that $T_*\mu=\nu$. Consequently, $f\mapsto f\circ T$ is an integral preserving embedding of $L^\infty (Z,\nu)$ into $L^\infty (X,\mu)$. Free transport extends this idea to non-commutative probability spaces (e.g. pairs $(A,\varphi)$ of von Neumann algebras/$C^*$-algebras and states) to produce state-preserving embeddings and even isomorphisms between non-commutative probability spaces. In this talk, we will discuss how to construct non-tracial transport by solving a non-commutative differential equation known as the Schwinger-Dyson equation and, time permitting, applications to $q$-deformed Araki-Woods algebras and finite depth subfactor planar algebras.
Talk Schedule:	Sunday 11/2, 12:00pm

Tron Omland, Arizona State University

Talk Title:	On simplicity and uniqueness of trace for reduced twisted group $C^*$-algebras
Talk Abstract:	In this talk, we consider pairs $(G,\sigma)$ of a discrete group $G$ and a two-cocycle $\sigma$ of $G$, and discuss sufficient conditions for the reduced twisted group $C^*$-algebra associated with $(G,\sigma)$ to be simple and/or have a unique tracial state. The topic has been studied a lot in the untwisted situation, where recent development (by Breuillard, Kalantar, Kennedy, and Ozawa) shows that uniqueness of trace for $C^*_r(G)$ is equivalent to $G$ having trivial amenable radical, which holds whenever $C^*_r(G)$ is simple. However, this result does not carry over to the twisted case, where also amenable groups play an important role. In particular, we will show that the twisted group $C^*$-algebras associated with so-called FC-hypercentral groups are simple (resp. have a unique tracial state) if and only if Kleppner's condition is satisfied (meaning that all nontrivial $\sigma$-regular conjugacy classes are infinite). The FC-hypercentral groups form a large subclass of elementary amenable groups containing for example all virtually nilpotent groups. Finally, by using a decomposition involving the FC-hypercenter of a group (which in any group is a normal subgroup), we can give conditions ensuring simplicity and/or uniqueness of trace for larger classes of groups. This is joint work with Erik Bedos (University of Oslo).
Talk Schedule:	Saturday 11/1, 11:00am

Raphael Ponge, Seoul National University/UC Berkeley

Talk Title:	Noncommutative geometry and conformal geometry: local index formula and conformal invariants.
Talk Abstract:	This will be report on a series of joint papers with Hang Wang (U. Adelaide, Australia). The general aim of these papers is to use tools from noncommutative geometry to study conformal geometry and some noncommutative incarnations of conformal geometry. In this talk, I will present two main results. The first main result is a reformulation of the local index formula in the setting of conformal-diffeomorphism invariant geometry. The second main result is the construction of a new family of global conformal invariants taking into account the action of the group of conformal-diffeomorphisms. These invariants are not of the same type as the conformal invariants considered by Spyros Alexakis in his celebrated solution of the Deser-Schwimmer. The arguments leading to both results heavily rely on noncommutative geometry. In particular, a crucial use is made of the conformal invariance of the Connes-Chern character. However, the main results are ultimately stated in differential-geometric fashion.
Talk Schedule:	Saturday 11/1, 2:00pm

Karen Strung, Institute of Mathematics, Polish Academy of Sciences

Talk Title:	Classification of C*-algebras of minimal homeomorphisms on odd dimensional spheres
Talk Abstract:	I will discuss my recent work on C*-algebras of products of minimal dynamical systems with Cantor minimal systems. In particular, I will show how taking such a product leads to the classification by tracial state spaces of the C*-algebras associated to minimal homeomorphisms on odd dimensional spheres.
Talk Schedule:	Saturday 11/1, 09:00am

Ami Viselter, University of Alberta, Canada & University of Haifa, Israel

Talk Title:	On positive definiteness over locally compact quantum groups
Talk Abstract:	Positive-definite functions over locally compact groups are a very fundamental tool in abstract harmonic analysis and related areas. They are tightly connected with various aspects of the group, such as representations, group properties (amenability and other approximation properties, property (T), etc.), the algebras associated to the group and many more. The concept of positive-definite functions in the setting of locally compact quantum groups (LCQGs) has lately appeared in a few papers in relation to other notions. This stimulated a very recent work of Daws and Salmi, in which they examined several ways to define "(completely) positive-definite functions over LCQGs", and proved that, under some mild assumptions, they are all equivalent. We continued this line of research, generalizing some known results about positive definiteness over groups to the quantum setting. These will be presented in the talk, after brief introductions to LCQGs and positive-definite functions. This is joint work with Volker Runde.
Talk Schedule:	Sunday 11/2, 10:00am

Rufus Willett, Univesity of Hawaii

Talk Title:	Exotic Crossed Products
Talk Abstract:	C*-algebraists usually consider two crossed products associated to a group action on a C*-algebra: the full crossed product and the reduced one. However, there are in general many other crossed products that come 'between' these two standard examples, and that capture interesting representation theoretic and dynamical properties of the group. I'll characterize some useful properties of exotic crossed products, and some examples that connect with representation theory. I'll also discuss which crossed product is the 'right' one to use in the Baum-Connes conjecture. Most of this is joint work with Alcides Buss and Siegfried Echterhoff, and some is joint work with Paul Baum and Erik Guentner.
Talk Schedule:	Saturday 11/1, 4:00pm

Zhizhang Xie, Texas A&M

Talk Title:	Higher Signature on Witt Spaces
Talk Abstract:	The signature is a fundamental homotopy invariant for topological manifolds. However, for spaces with singularities, this usual notion of signature ceases to exist, since, in general, spaces with singularities fail the usual Poincar\'{e} duality. A generalized Poincar\'{e} duality theorem for spaces with singularities was proven by Goresky and MacPherson using intersection homology. The classical signature was then extended to Witt spaces by Siegel using this generalized Poincar\'{e} duality. Witt spaces are a natural class of spaces with singularities. For example, all complex algebraic varieties are Witt spaces. In this talk, I will describe a combinatorial approach to the higher signature of Witt spaces, using methods of operator algebras. This is based on joint work with Nigel Higson.
Talk Schedule:	Saturday 11/1, 5:00pm